ここでは DXF の SPLINE で定義される情報から,なめらかな曲線座標を再現する方法を紹介します.
落合重紀著:DXFハンドブック第2版,オーム社(H25)より,数式を定義します.
\[P(t)=\sum^{n-1}_{i=0} Q_i N_{i,m}(t)\]
| $Q_i$ | 制御点 | |
| $N_{i,m}(t)$ | 基底関数 | |
| $n$ | 制御点の数 | 文献では $n+1$ となっていますが $n$ のほうがわかりやすい |
| $m$ | 階数 | 次数+1 通常DXFのBスプラインは3次らしいので階数は4になります |
基底関数は \begin{eqnarray} N_{i,1}(t)&=&\left\{ \begin{matrix}1&t_i\leq t < t_{i+1} \,^{*1} \\ 0&\mathrm{other} \end{matrix} \right. \\ N_{i,m}(t)&=&\frac{t-t_i}{t_{i+m-1}-t_i}N_{i,m-1}(t)+\frac{t_{i+m}-t}{t_{i+m}-t_{i+1}}N_{i+1,m-1}(t) \end{eqnarray}
(*1)文献では $t_i\leq t \leq t_{i+1}$ ですが,$t=t_{i+1}$ のときに計算結果がおかしくなったので上記のようにしています.
$t_i$ はノット(重ね合わせ,多重度)で,ノットベクトルは
\[T=\{t_0=t_1=\cdots = t_{m-1} < t_m \leq t_{m+1} \leq \cdots \leq t_n < t_{n+1} = \cdots = t_{n+m}\}\]
以上のことを考慮して作成したPythonプログラム spline.py が以下の通り.参考URLはhttp://maicommon.ciao.jp/ss/Jalgo/Bspline/index.htm
$t$はノットベクトルの最小値と最大値の間を100分割しました.曲線の滑らかさに関わります.
import numpy as np
def baseN(i, m, t, nv):
if m == 1:
if nv[i] <= t < nv[i+1]:
return 1.0
else:
return 0.0
b = nv[i+m-1] - nv[i]
if b != 0:
w1 = (t-nv[i]) / b * baseN(i, m-1, t, nv)
else:
w1 = 0
b = nv[i+m] - nv[i+1]
if b != 0:
w2 = (nv[i+m]-t) / b * baseN(i+1, m-1, t, nv)
else:
w2 = 0
return w1+w2
lqx, lqy = np.loadtxt("q.txt", unpack=True)
nv = np.loadtxt("nv.txt")
tmin = min(nv)
tmax = max(nv)
px = []
py = []
for t in np.linspace(tmin, tmax, 100):
i = 0
x = 0
y = 0
if t==tmax: # これがないと
t -= 0.001 # 終点までいかない
for qx, qy in zip(lqx, lqy):
r = baseN(i, 4, t, nv)
x += qx * r
y += qy * r
i += 1
if x!=0 or y!=0:
px.append(x)
py.append(y)
for x, y in zip(px, py):
print(str(x)+','+str(y))
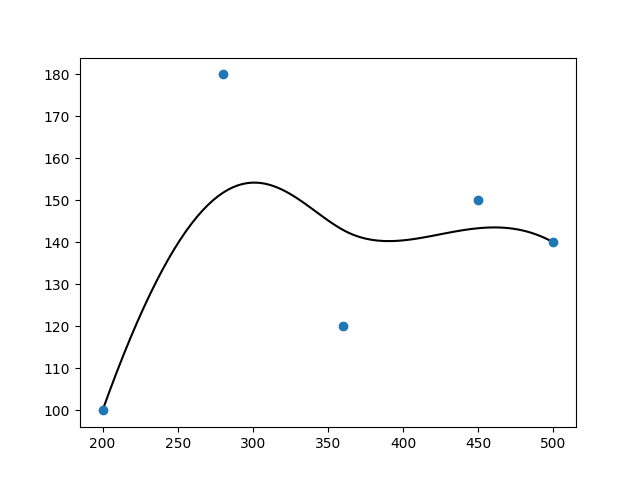
制御点情報 q.txt は
200.0 100.0
280.0 180.0
360.0 120.0
450.0 150.0
500.0 140.0
ノットベクトル nv.txt は
0.0
0.0
0.0
0.0
1.0
2.0
2.0
2.0
2.0
グラフ作成用のプログラム graph.py
import numpy as np
import fileinput
import matplotlib.pyplot as plt
dx, dy = np.loadtxt(fileinput.input(), delimiter=',', unpack=True)
qx, qy = np.loadtxt("q.txt", unpack=True)
plt.plot(dx, dy, c='k')
plt.plot(qx, qy, 'o')
plt.show()
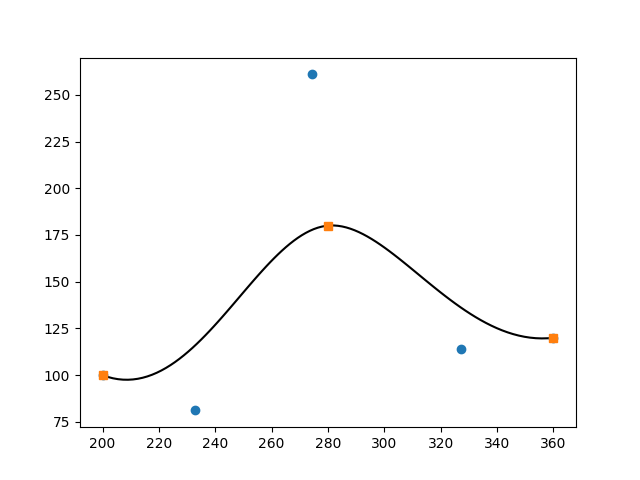
コマンドプロンプトで py spline.py | py graph.py とすると以下のグラフが作成できます.青丸が制御点です.
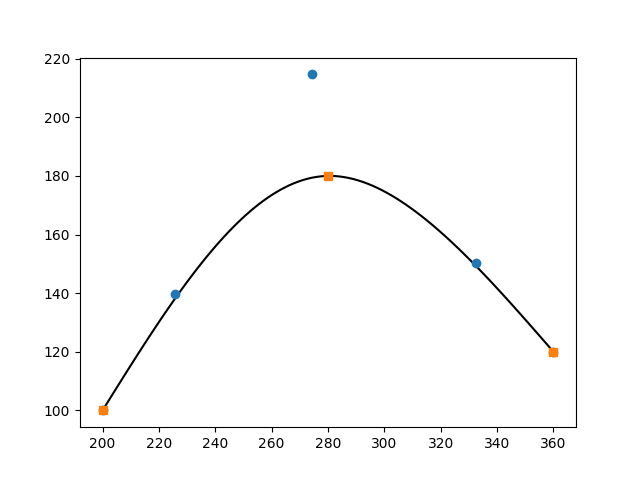
「次数+1だけ重ねるとその点を通る」らしいのですが,計算方法がわかりません.
制御点情報 q2.txt は
200.0 100.0
225.7368791538797 139.7497698097172
274.2221605281183 214.6337073482535
332.6069368389686 150.2211743305082
360.0 120.0
ノットベクトル nv2.txt
0.0
0.0
0.0
0.0
113.1370849898476
213.1370849898476
213.1370849898476
213.1370849898476
213.1370849898476
フィット点 fit2.txt
200.0 100.0
280.0 180.0
360.0 120.0
これでグラフ化(graph.pyの変更点は省略)すると以下のグラフになります. 橙色がフィット点ですが,とくに計算で細工しなくてもノットベクトルの情報だけでその点にフィットしているようです.
文献には式が書かれていませんでした.調査したところ制御点に重みを付けるらしいので,最初の式が
\[P(t)=\sum^{n-1}_{i=0} Q_i w_i N_{i,m}(t)\]
| $w_i$ | 重み |
になります.重みを読み込むように spline.py を変更します.
import numpy as np
def baseN(i, m, t, nv):
if m == 1:
if nv[i] <= t < nv[i+1]:
return 1.0
else:
return 0.0
b = nv[i+m-1] - nv[i]
if b != 0:
w1 = (t-nv[i]) / b * baseN(i, m-1, t, nv)
else:
w1 = 0
b = nv[i+m] - nv[i+1]
if b != 0:
w2 = (nv[i+m]-t) / b * baseN(i+1, m-1, t, nv)
else:
w2 = 0
return w1+w2
lqx, lqy, lw = np.loadtxt("q3.txt", unpack=True)
nv = np.loadtxt("nv3.txt")
tmin = min(nv)
tmax = max(nv)
px = []
py = []
for t in np.linspace(tmin, tmax, 100):
i = 0
x = 0
y = 0
if t==tmax:
t -= 0.001
for qx, qy, w in zip(lqx, lqy, lw):
r = baseN(i, 4, t, nv)
x += qx * r * w
y += qy * r * w
i += 1
if x!=0 or y!=0:
px.append(x)
py.append(y)
for x, y in zip(px, py):
print(str(x)+','+str(y))
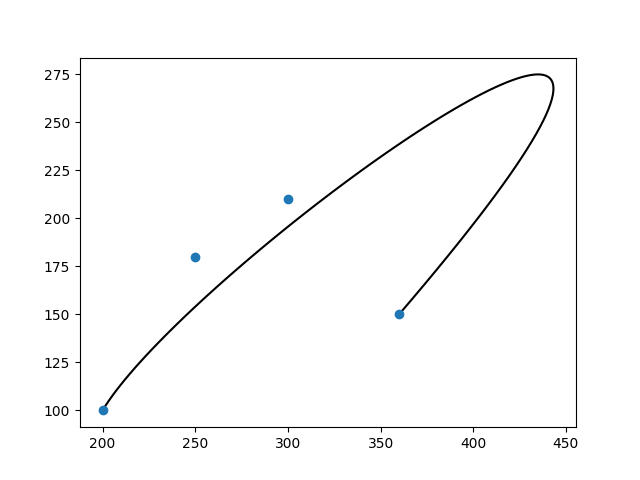
制御点情報 q3.txt は,3列目に重み情報を追加します.
200.0 100.0 1.0
250.0 180.0 1.0
300.0 210.0 2.0
360.0 150.0 1.0
ノットベクトル nv3.txt
0.0
0.0
0.0
0.0
1.0
1.0
1.0
1.0
これでグラフ化すると,以下のようになりました.文献の曲線とずいぶん違います.式の定義がまちがってるのかな?
まさか文献の曲線が間違えてる??
もし正解をご存じの方がいれば,サポート掲示板のトピックにコメントいただけると幸いです.
制御点情報 q4.txt
1150.0 525.0 1.0
1166.666666666666 550.0 1.0
1100.0 650.0 1.0
1000.0 500.0 1.0
1133.333333333333 500.0 1.0
1150.0 525.0 1.0
ノットベクトル nv4.txt
0.0
0.0
0.0
0.0
1.0
2.0
3.0
3.0
3.0
3.0
とくにアルゴリズムを変更することなく,うまくいっているようです.
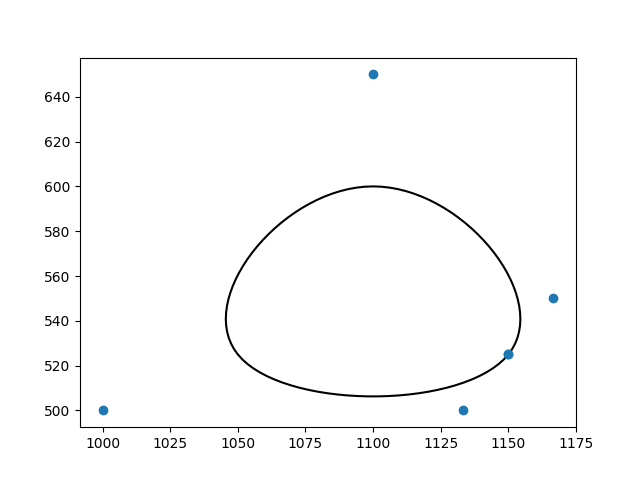
連続ではない閉じたスプラインの場合,制御点情報 q5.txt
1000.0 500.0 1.0
1200.0 500.0 1.0
1100.0 650.0 1.0
1000.0 500.0 1.0
ノットベクトル nv5.txt
0.0
0.0
0.0
0.0
1.0
1.0
1.0
1.0
これもとくに問題なさそうです.
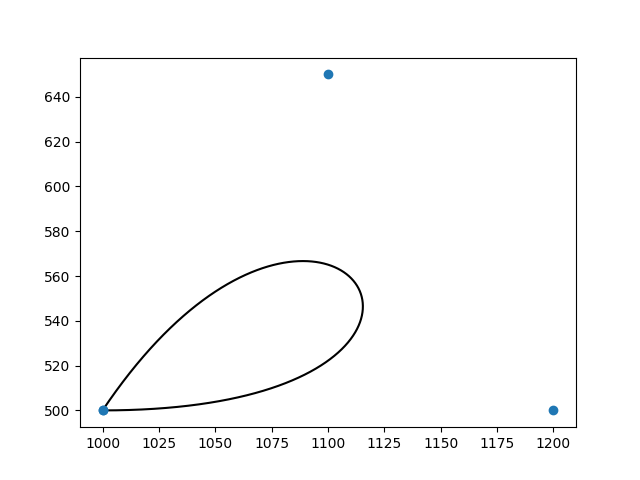
DXFのスプラインでは,開始点終了点の接線単位ベクトルが指示できるようですが,その分制御点が増えているので同じアルゴリズムでいけるのかな?.
制御点情報 q6.txt
200.0 100.0 1.0
232.6598632371091 81.14381916835874 1.0
274.2364614088482 260.9041393287876 1.0
327.1730748995931 114.2117274111023 1.0
360.0 120.0 1.0
接線ベクトル情報は省略します.ノットベクトルとフィット点は[フィット点のあるスプライン]nv2.txt, fit2.txtと同じです.とくに問題なさそうです.